“原始分回归分析”的版本间的差异
来自成绩云帮助中心
| 第2行: | 第2行: | ||
直接对比每个学校的均分和上一次考试的均分是不科学的,因为两次考试的卷面难度不一致。在分值上可能某个学校有减少,但是实际上可能是获得了进步。<br> | 直接对比每个学校的均分和上一次考试的均分是不科学的,因为两次考试的卷面难度不一致。在分值上可能某个学校有减少,但是实际上可能是获得了进步。<br> | ||
回归分析可以解决这样的情景:<br> | 回归分析可以解决这样的情景:<br> | ||
| − | + | 回归的公式是 y = a*x + b;<br> | |
| − | + | 每个单科,以上次考试作为自变量x,本次成绩为因变量y,每个学校为一个数据点,通过回归算法确定出参数a和b,(下图中,a = 2.1948, b = -95.36)<br> | |
| − | 然后计算y- | + | 把上次考试的分数再作为x值代入函数算出y0,即回归值,把这些回归值连成线,就是下图中的斜线,斜线对应每个x的y值就是指,上一次考试的某个分数,放到这次考试来等同于多少分。<br> |
| + | 然后计算y-y0,得出该校在该科的回归比较值。这个比较值就是散点到线的Y轴差距,也就是该学校本次的均分相对于上次而言,实际的进退步。<br> | ||
[[文件:回归分析示例图.png|border]] | [[文件:回归分析示例图.png|border]] | ||
2016年5月1日 (日) 02:58的版本
在统考的分析中,如果我们想知道学校均分的进退步情况,该如何对比呢?
直接对比每个学校的均分和上一次考试的均分是不科学的,因为两次考试的卷面难度不一致。在分值上可能某个学校有减少,但是实际上可能是获得了进步。
回归分析可以解决这样的情景:
回归的公式是 y = a*x + b;
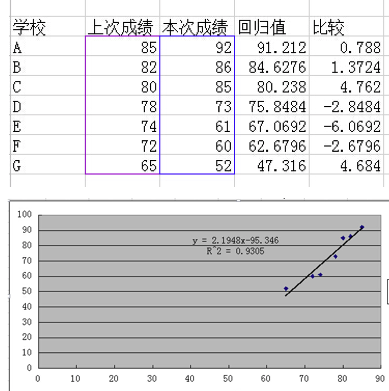
每个单科,以上次考试作为自变量x,本次成绩为因变量y,每个学校为一个数据点,通过回归算法确定出参数a和b,(下图中,a = 2.1948, b = -95.36)
把上次考试的分数再作为x值代入函数算出y0,即回归值,把这些回归值连成线,就是下图中的斜线,斜线对应每个x的y值就是指,上一次考试的某个分数,放到这次考试来等同于多少分。
然后计算y-y0,得出该校在该科的回归比较值。这个比较值就是散点到线的Y轴差距,也就是该学校本次的均分相对于上次而言,实际的进退步。